2021.06.16
Eyedropper Tool Helpful Tips – Difference between Canvas and Layer –

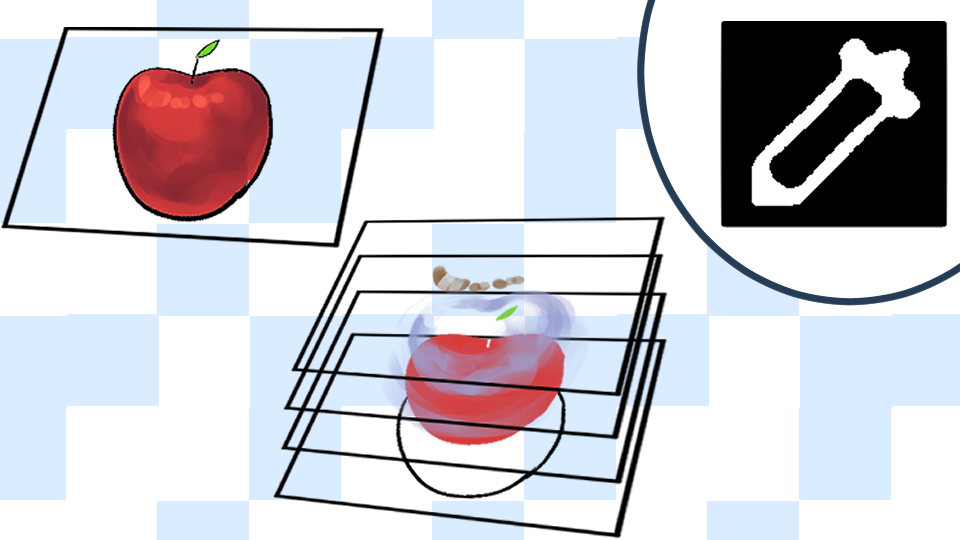
In this article, I will explain the difference between “canvas” and “layer” in the reference section as a useful knowledge of the eyedropper tool.
Index
What is the eyedropper tool
The eyedropper tool is a feature that allows you to select a color in the canvas and extract that color to the foreground color of the color window.
There are two references to the eyedropper tool: “canvas” and “layer”.
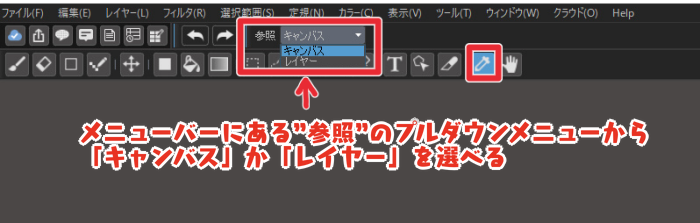
You can use this canvas and layers to make your drawing more efficient.
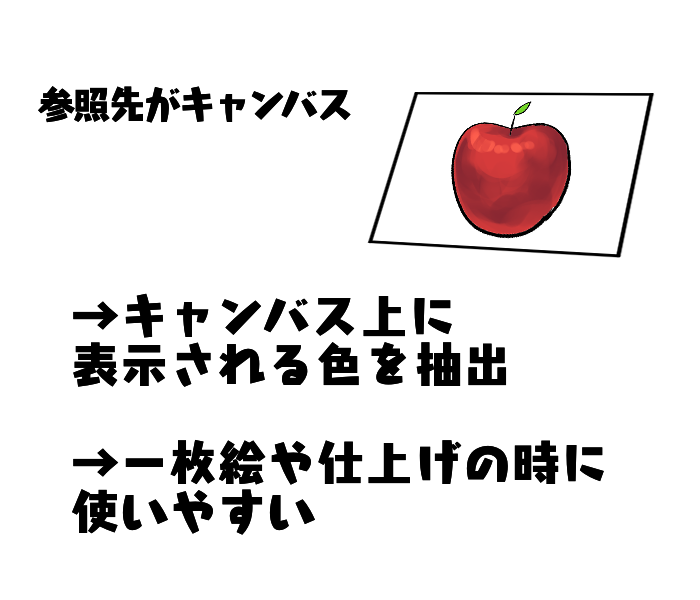
Reference to Canvas
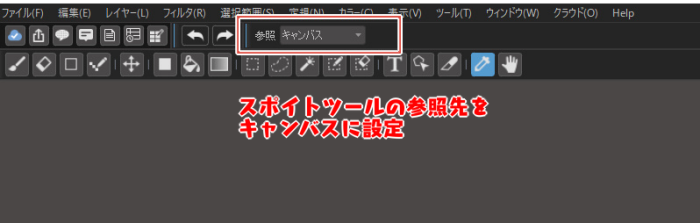
If you set the eyedropper tool’s reference to the canvas, you can extract a color that reflects the colors of all the layers displayed at the specified location.
Simply put, it is possible to extract the color that is visible on the canvas.
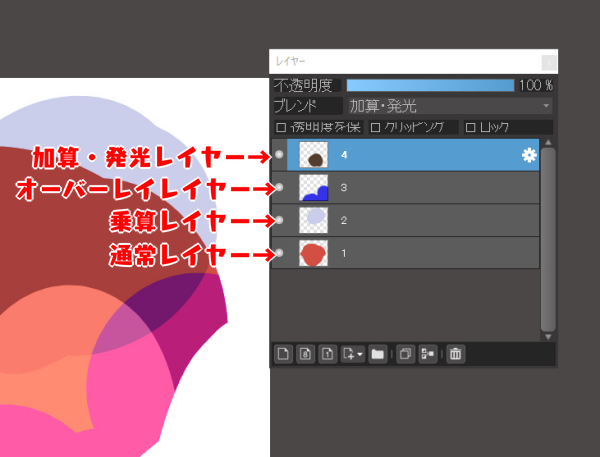
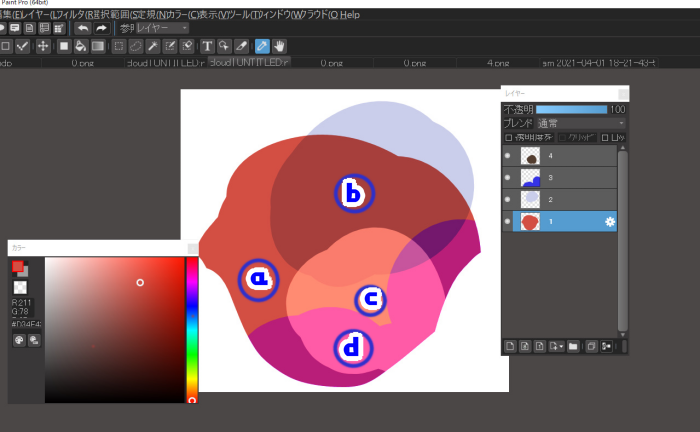
For example, let’s say you have a layer of colors as shown below.

The layer structure looks like this
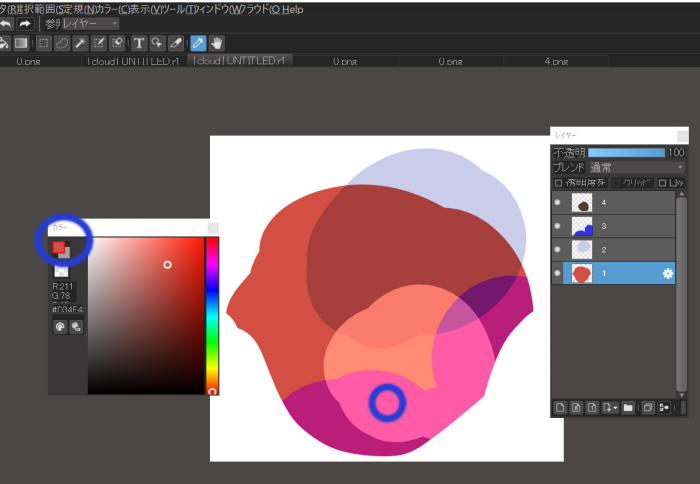
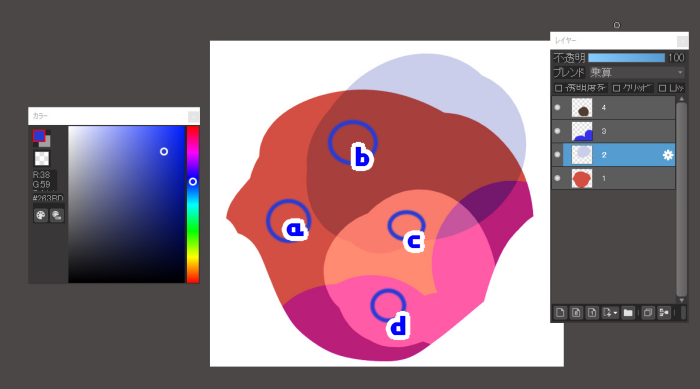
From here, use the eyedropper tool to select the a, b, c, and d areas.
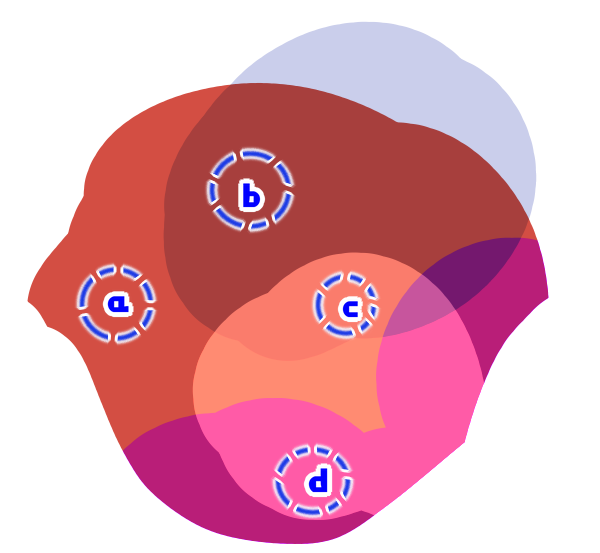
Notice the color of the color window when you dropper the respective part.
Eyedropping the “a” part
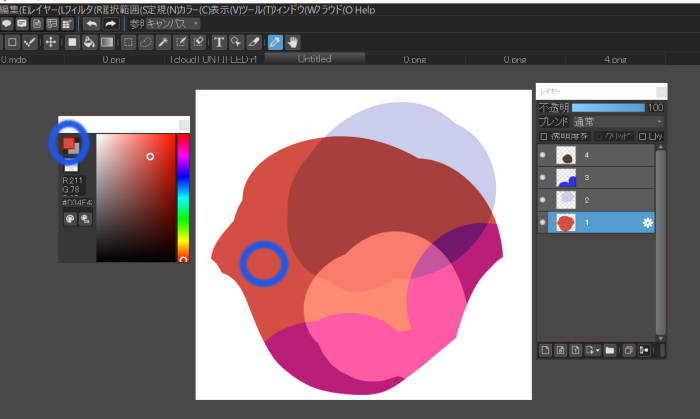
Eyedropper at “b
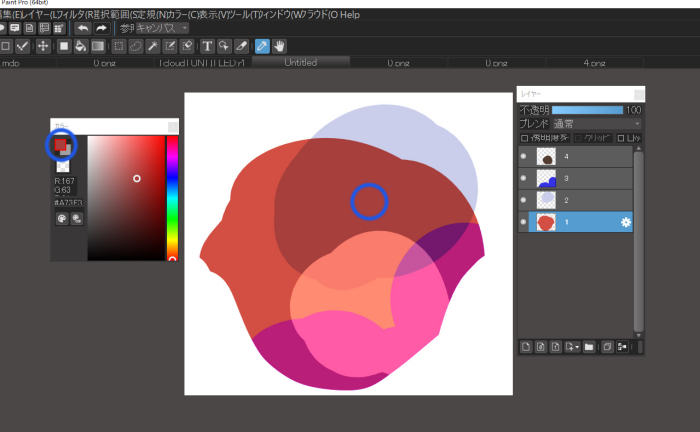
Eyedropper at c
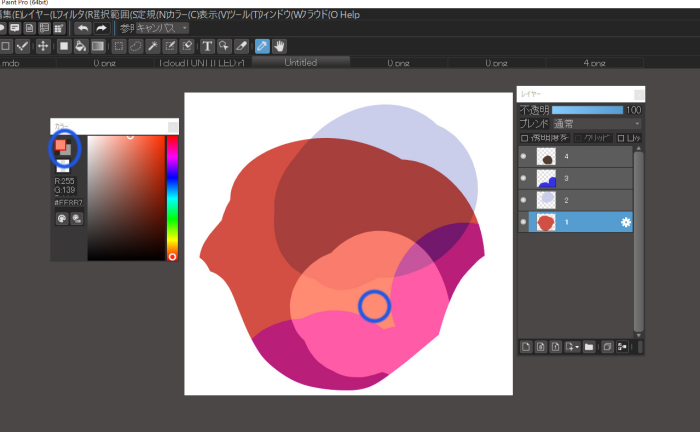
Eyedropper at “d
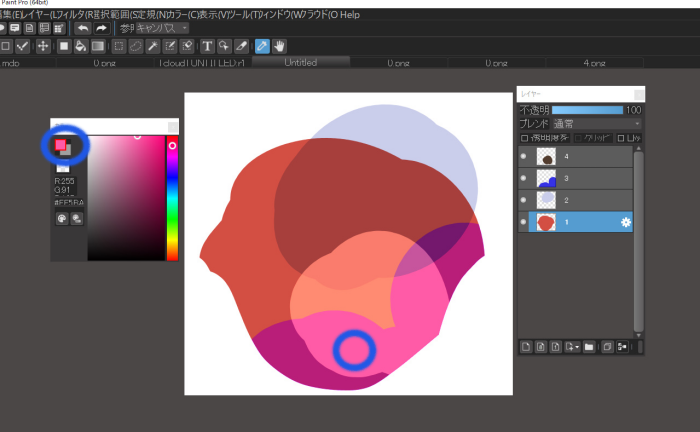
In both cases, you can see that the colors are extracted to reflect the colors and blends of each of the layers in the spot where you dropper.
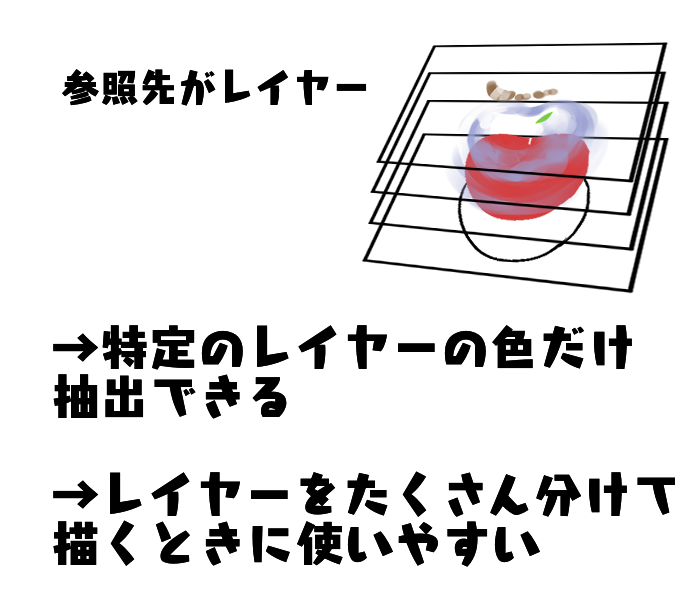
Reference as a layer
Next, let’s look at the case where a reference is set to a layer.
In this case, only the colors drawn on the selected layer will be imported.
Using a normal layer as a reference
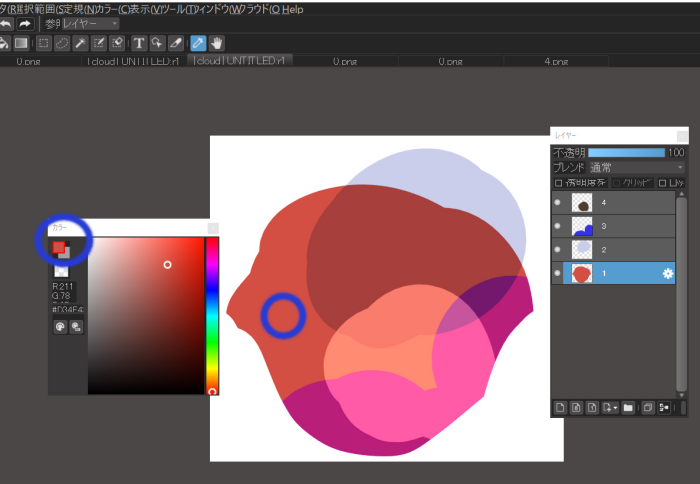
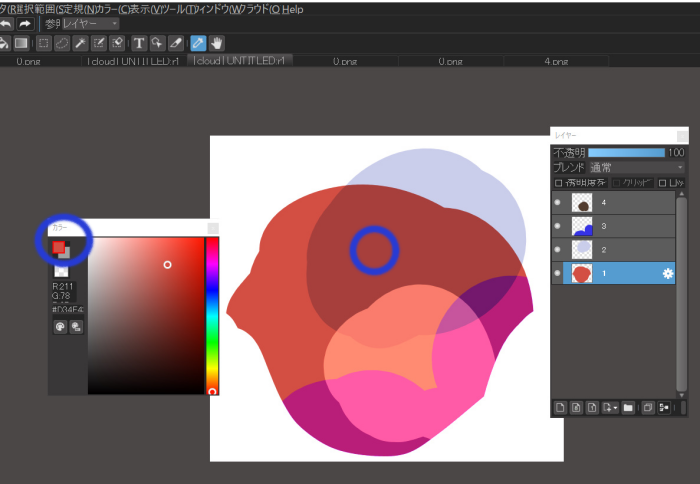
Let’s try selecting layer 1 and using the eyedropper tool, take the colors of points a, b, c, and d.
Notice the foreground color in the color window.
Eyedropper for the “a” part
Eyedropper for the “b” part
Eyedropper for the “c” part
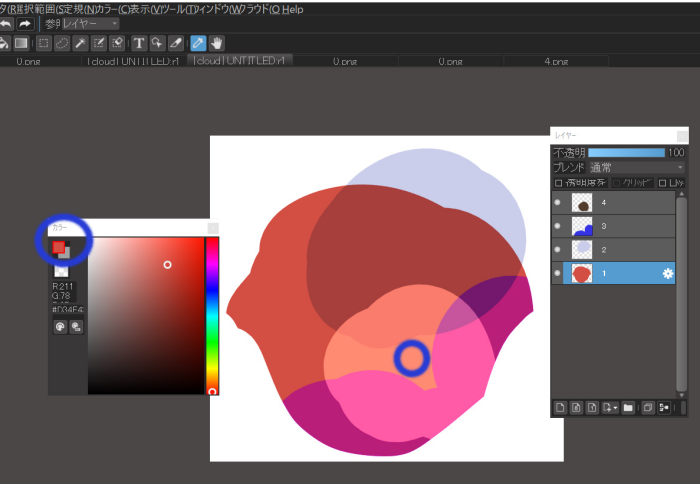
Eyedropper for the “d” spot
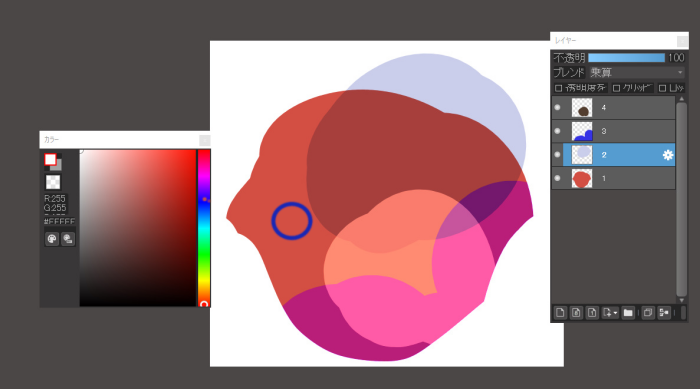
In this case, the same color will be extracted no matter which part of the image is used.
This is because the eyedropper tool extracts colors only from the drawing on layer 1.
By the way, if you use the eyedropper on a blank space, white will be extracted.
Multiplication layer as a reference
Let’s look at the case where the multiply layer is used as a reference.
As before, let’s eye-dropper a, b, c, and d.
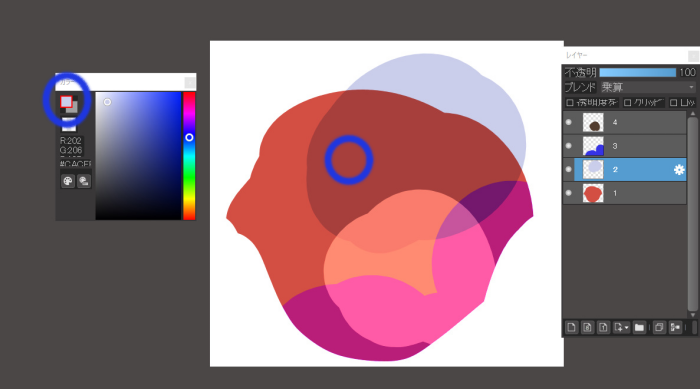
Eyedropper for the “a” spot
Eyedropper for the “b” part
Eyedropper for the “c” part
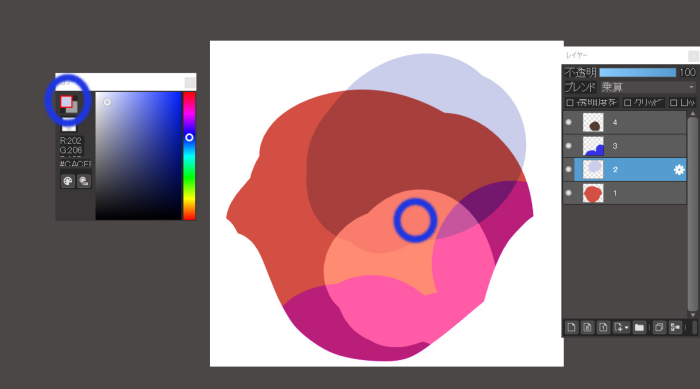
Eyedropper at “d

In a and d, there is no depiction of layer 2, so white is reflected.
In contrast, we can see that b and c extract only the colors drawn on layer 2.
Note that if you set the Layer Blend to something other than the usual effects, such as Multiply or Overlay, the colors you see will be different from the colors you actually draw on the canvas.
Use the eyedropper tool with different references!
If you use the eyedropper tool’s reference as a canvas, it can be useful for extracting colors from a picture that has been merged into a single piece, or for applying colors as a finishing touch.
Also, if you use a layer as a reference, layer referencing is useful when you draw on many separate layers, or when you want to extract only the colors of a particular layer.
By changing the eyedropper tool’s reference, you can make your drawing more efficient, so I encourage everyone to take advantage of this feature!
Here are some useful techniques for using the eyedropper tool
An easy technique to fill in the gaps in a bucket of paint.
(Text and pictures by Setsu Yoshida)
\ We are accepting requests for articles on how to use /